250x250
Notice
Recent Posts
Recent Comments
Link
반응형
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 큐
- 리소스모니터링
- math
- string
- javascript
- 힙덤프
- scanner
- GC로그수집
- CSS
- NIO
- spring boot
- sql
- html
- 스프링부트
- date
- deque
- Union-find
- 스택
- alter
- Calendar
- set
- List
- priority_queue
- BFS
- map
- Java
- Properties
- JPA
- union_find
- dfs
Archives
- Today
- Total
매일 조금씩
이코테 DP : 효율적인 화폐 구성 [C++] 본문
728x90
반응형



한 재작년이나 작년쯤 뭣도 모르고 코테를 쳤을 때.. 이런비슷한 문제들을 많이 봤다.
다이나믹 프로그래밍을 몰랐기 때문에 가장 큰 화폐단위부터 나누어 떨어지느냐 아니냐로 매달리다가 포기했던 기억이있다...
위의 문제 해결 아이디어를 보면 점화식으로 문제를 해결하는것과 같다.
아래와 같이 인덱스 값이 나오기 위한 결과값을 담을 배열을 만든다.
그 배열은 M의 최댓값이 10000이므로 크기가 M+1이고 초깃값이 전부 10001인 배열이다.
0은 어떠한 화폐단위로도 만들 수 없으므로 인덱스가 0인 자리엔 0을 넣는다.

다음 화폐 단위가 작은 것부터 반복문을 돌린다.
반복문이 시작은 화폐단위이고 끝은 M이 된다.
예를 들어, 아래처럼 화폐단위가 2이고 M이 7일 때 2부터 7까지가 된다.
아래는 화폐단위 2에 대한 반복문을 돌린 직후의 결과값 배열이다.
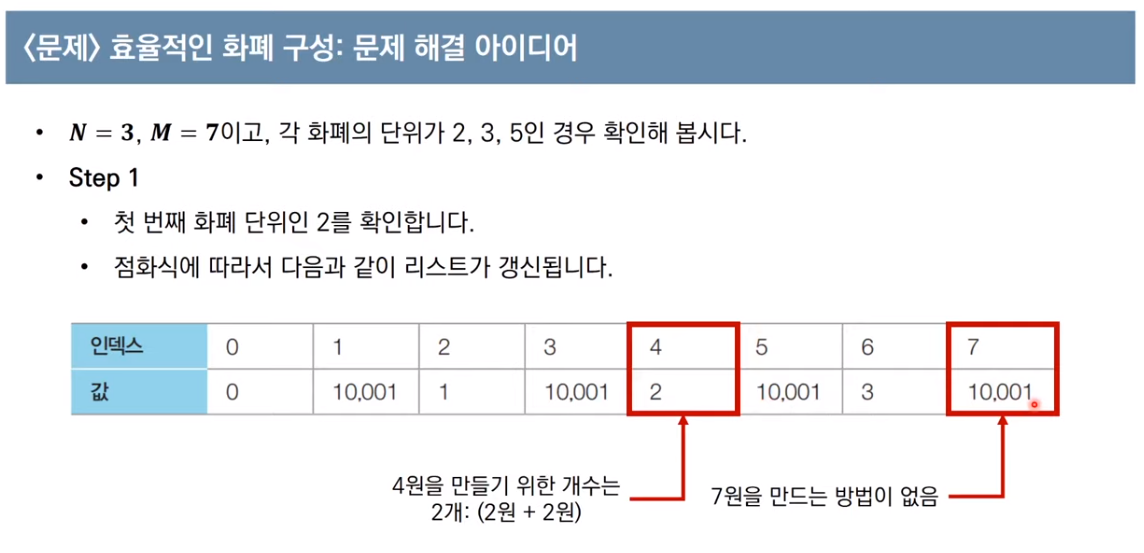
아래는 화폐단위 3에 대한 반복문을 돌린 후 결과값 배열이다.

다음은 마지막 화폐 단위인 5에 대한 반복문을 돌린 후 결과값 배열이다.

이렇게 문제를 해결하면 단순히 큰단위에서 나누어서 해결하려는 아이디어보다 나머지 잔금 처리가 쉽다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n, m;
vector<int> arr;
int main(void) {
// 정수 N, M을 입력받기
cin >> n >> m;
// N개의 화폐 단위 정보를 입력 받기
for (int i = 0; i < n; i++) {
int x;
cin >> x;
arr.push_back(x);
}
// 한 번 계산된 결과를 저장하기 위한 DP 테이블 초기화
vector<int> d(m + 1, 10001);
// 다이나믹 프로그래밍(Dynamic Programming) 진행(보텀업)
d[0] = 0;
for (int i = 0; i < n; i++) {
for (int j = arr[i]; j <= m; j++) {
// (i - k)원을 만드는 방법이 존재하는 경우
if (d[j - arr[i]] != 10001) {
d[j] = min(d[j], d[j - arr[i]] + 1);
}
}
}
// 계산된 결과 출력
if (d[m] == 10001) { // 최종적으로 M원을 만드는 방법이 없는 경우
cout << -1 << '\n';
}
else {
cout << d[m] << '\n';
}
}
728x90
반응형
'알고리즘 > DP' 카테고리의 다른 글
| Leet code (Medium) : 139. Word Break - JAVA (0) | 2024.10.13 |
|---|---|
| Leet code (Medium) : 322. Coin Change - JAVA (0) | 2024.10.13 |
| 이코테 DP : 병사 배치하기 [C++] (0) | 2021.05.13 |
| 이코테 DP : 금광 [C++] (0) | 2021.04.28 |
| 이코테 DP : 개미 전사 [C++] (0) | 2021.04.23 |




